FUNCIONES PERIÓDICAS.
Función que repite el mismo valor a intervalos regulares de la variable.
Una función f(x) es periódica si existe un número p tal que pueda hacer f(x+p) = f(x) para todas las x. Al menor número p se le llama período. Por ejemplo, y = sen (x) es una función periódica con un período de 2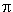
porque 2 es el menor número p que hace que s.
porque 2 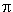es el menor número p que hace que s.
En matemáticas, una función es una función periódica si los valores de la variable dependiente se repiten conforme se va añadiendo a la variable indepediente un determinado período.
Por ejemplo: en la vida diaría existen muchos casos de funciones periódicas cuando la variable es el tiempo; situaciones como el movimiento de las manecillas de un reloj o las fases de la luna muestran un comportamiento periódico. Un movimiento periódico es un movimiento en el que la posición(es) del sistema se pueden expresar en base a funciones periódicas, todas con el mismo período.
Para una función aplicada al conjunto de los números reales o al de los enteros, significa que la totalidad de su gráfica puede ser representada a partir de copias de una determinada porción de ésta, repetida a intervalos regulares.
De forma más explícita, se dice que una función f es periódica con período P mayor que cero si cumple que
para todos los valores de x en el dominio de f. De manera análoga, una función no periódica es aquella que no posee dicho período P.
F(x+p)=F(x)
Por ejemplo: en la vida diaría existen muchos casos de funciones periódicas cuando la variable es el tiempo; situaciones como el movimiento de las manecillas de un reloj o las fases de la luna muestran un comportamiento periódico. Un movimiento periódico es un movimiento en el que la posición(es) del sistema se pueden expresar en base a funciones periódicas, todas con el mismo período.
Para una función aplicada al conjunto de los números reales o al de los enteros, significa que la totalidad de su gráfica puede ser representada a partir de copias de una determinada porción de ésta, repetida a intervalos regulares.
De forma más explícita, se dice que una función f es periódica con período P mayor que cero si cumple que
para todos los valores de x en el dominio de f. De manera análoga, una función no periódica es aquella que no posee dicho período P.
F(x+p)=F(x)
Las funciones seno, coseno y tangente , cuyas imágenes anotaremos sen(x), cos(x) y tg(x) , son ejemplos de funciones periódicas.
El seno (abreviado como sen, o sin por llamarse "sinus" en latín) es la razón entre el cateto opuesto y la hipotenusa,
El coseno (abreviado como cos) es la razón entre el cateto adyacente y la hipotenusa.
