
Clasificación de funciones Funciones algebraicas
En las funciones algebraicas las operaciones que hay que efectuar con la variable independiente son: la adición, sustracción, multiplicación, división, potenciación y radicación.
Las funciones algebraicas pueden ser:
Funciones explícitas
Si se pueden obtener las imágenes de x por simple sustitución.
f(x) = 5x − 2
Funciones implícitas
Si no se pueden obtener las imágenes de x por simple sustitución, sino que es preciso efectuar operaciones.
5x − y − 2 = 0
Funciones polinómicas
Son las funciones que vienen definidas por un polinomio.
f(x) = a0 + a1x + a2x² + a2x³ +··· + anxn
Su dominio es  , es decir, cualquier número real tiene imagen.
, es decir, cualquier número real tiene imagen.
 , es decir, cualquier número real tiene imagen.
, es decir, cualquier número real tiene imagen.Funciones constantes
El criterio viene dado por un número real.
f(x)= k
La gráfica es una recta horizontal paralela a al eje de abscisas.
Funciones polinómica de primer grado
f(x) = mx +n
Su gráfica es una recta oblicua, que queda definida por dos puntos de la función.
Funciones cuadráticas
f(x) = ax² + bx +c
Son funciones polinómicas es de segundo grado, siendo su gráfica una parábola.
Funciones a trozos
Son funciones definidas por distintos criterios, según los intervalos que se consideren.
Funciones racionales
El criterio viene dado por un cociente entre polinomios:

El dominio lo forman todos los números reales excepto los valores de x que anulan el denominador.
Funciones radicales
El criterio viene dado por la variable x bajo el signo radical.
El dominio de una función irracional de índice impar es R.
El dominio de una función irracional de índice par está formado por todos los valores que hacen que el radicando sea mayor o igual que cero.
Funciones trascendentes
La variable independiente figura como exponente, o como índice de la raíz, o se halla afectada del signo logaritmo o de cualquiera de los signos que emplea la trigonometría.
Función exponencial
Sea a un número real positivo. La función que a cada número real x le hace corresponder la potencia ax se llamafunción exponencial de base a y exponente x.
Funciones logarítmicas
La función logarítmica en base a es la función inversa de la exponencial en base a.
Funciones trigonométricas
Función seno
f(x) = sen x
Función coseno
f(x) = cos x
Función tangente
f(x) = tg x
Función cosecante
f(x) = cosec x
Función secante
f(x) = sec x
Función cotangente
f(x) = cotg x
En matemática, Relación es la correspondencia de un primer conjunto, llamado Dominio, con un segundo conjunto, llamadoRecorrido o Rango, de manera que a cada elemento del Dominio le corresponde uno o más elementos del Recorrido o Rango.
Por su parte, una Función es una relación a la cual se añade la condición de que a cada valor del Dominio le corresponde uno y sólo un valor del Recorrido.
Por su parte, una Función es una relación a la cual se añade la condición de que a cada valor del Dominio le corresponde uno y sólo un valor del Recorrido.
De las definiciones anteriores podemos deducir que todas las funciones son relaciones, pero no todas las relaciones sonfunciones.
También debemos agregar que toda ecuación es una Relación, pero no toda ecuación es una Función.
Todas las Relaciones pueden ser graficadas en el Plano Cartesiano.
Dominio, codominio y rango
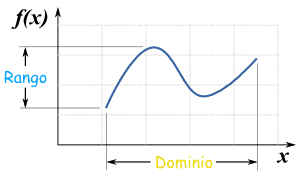 |
En su forma más simple el dominio son todos los valores a los que aplicar una función, y el rango son los valores que resultan.
|
Funciones
Una función relaciona una entrada con una salida.
Entrada y salida
Pero muchas veces es importante decir qué valores pueden entrar y pueden salir de una función.
- La función no funciona si das valores equivocados (como una edad negativa)
- Limitar los valores de entrada te puede permitir hacer después cosas especiales con la función
- Saber el tipo de valores de salida (por ejemplo siempre positivos) también ayuda
Dominio y rango
Hay nombres especiales para lo que puede entrar, y también lo que puede salir de una función:
 | Lo que puede entrar en una función se llama el dominio |
 | Lo que es posible que salga de una función se llama el codominio |
 | Lo que en realidad sale de una función se llama rango o imagen |
Entonces, en el diagrama de arriba el conjunto "X" es el dominio, el conjunto "Y" es el codominio, y los elementos de Y a los que llegan flechas (los valores producidos realmente por la función) son el rango.
Parte de la función
Lo que sale (el rango) depende de lo que pones (el dominio), pero TÚ defines el dominio.
De hecho el dominio es una parte esencial de la función. Un dominio diferente da una función diferente.
El codominio y el rango tienen que ver con la salida, pero no son exactamente lo mismo.
El codominio es el conjunto de valores que podrían salir.
El rango es el conjunto de valores que realmente salen.
Imagen:
Son todos los puntos de la gráfica de la función a los que les corresponde un valor en Y.
Regla de Correspondencia:
La regla de correspondencia es como decir y = 2x o escrito de otra manera: f(x) = 2x
lo cual significa que el valor de y depende del valor de x o que el valor de y responde a esa regla
entonces en ese caso la regla de correspondencia seria
que a cada valor de x le corresponde un valor de y y el valor de y debe ser igual al valor de x multiplicado por 2, así para cada numero de x se puede elaborar una tabla
x le corresponde y
1 le corresponde 2
2 le corresponde 4
3 le corresponde 6
y así sucesivamente con todos los valores de x te sigues con el 4 y le corresponde el 8
Así cada función es una regla de correspondencia otro ejemplo y = x²
la regla es que cada valor de x le corresponde un valor de y, y el valor de y es igual a lo que valga x elevado al cuadrado así puedes seguir elaborando la tabla al uno le corresponde el uno al dos el cuatro al tres el nueve y así sucesivamente.
lo cual significa que el valor de y depende del valor de x o que el valor de y responde a esa regla
entonces en ese caso la regla de correspondencia seria
que a cada valor de x le corresponde un valor de y y el valor de y debe ser igual al valor de x multiplicado por 2, así para cada numero de x se puede elaborar una tabla
x le corresponde y
1 le corresponde 2
2 le corresponde 4
3 le corresponde 6
y así sucesivamente con todos los valores de x te sigues con el 4 y le corresponde el 8
Así cada función es una regla de correspondencia otro ejemplo y = x²
la regla es que cada valor de x le corresponde un valor de y, y el valor de y es igual a lo que valga x elevado al cuadrado así puedes seguir elaborando la tabla al uno le corresponde el uno al dos el cuatro al tres el nueve y así sucesivamente.
EJERCICIOS:
Calcular el dominio de las funciones racionales:
1 
3 
4
5 
6 
7
8 
9 
10 
11
12
13
14
115

16
17 
18
19 
20
21 
22
funciones continuas y discontinuas
Son aquellas gráficas que no presentan ningún punto aislado, saltos o interrupciones y que están hechas de un sólo trazo en un intervalo determinado son llamadas funciones continuas.
Función Discontinua
Las gráficas que presentan algún punto aislado, saltos o interrupciones, es decir, que no están hechas de un sólo trazo en un intervalo determinado, son llamadas funciones discontinuas.
Función Sobreyectiva:
También se la llama suryectiva y es aquella función en que todos los valores de "y" (el codominio) son imágen de un valor de "x" (el dominio).
. Para darte un ejemplo, una 'parábola no es suryectiva porque desde el vértice en más todos los valores de "y" no son imágen de ninguna "x" ( f(x)=x^2, todas las y menores que cero no son imágen de ningún valor de x, otra, f(x)=senx , todas las y mayores que uno o menores que menos uno no son imágen)
, Ejemplos de suryectividad, f(x)=mx+b , todos los valores de Y son imágen de f.
. Para darte un ejemplo, una 'parábola no es suryectiva porque desde el vértice en más todos los valores de "y" no son imágen de ninguna "x" ( f(x)=x^2, todas las y menores que cero no son imágen de ningún valor de x, otra, f(x)=senx , todas las y mayores que uno o menores que menos uno no son imágen)
, Ejemplos de suryectividad, f(x)=mx+b , todos los valores de Y son imágen de f.
Funcion Biyectiva:
una funcion inyectiva es aquella funcion la cual, para todos los elementos de un conjunto B (por ej) llamado conjunto imagen, le corresponde un solo elemento del conjunto A que podemos llamarle dominio de la funcion, por ej:
y=5x+2
es una funcion inyectiva, ya que cada valor de y le hace corresponder un solo valor de x,
y=x²
no es una funcion inyectiva, ya que para un determinado valor de y le corresponde 2 valores de x del dominio, por lo tanto podemos hacer una reestriccion del conjunto del dominio de manera que sea inyectiva, haciendo
Domfuncion: x≥0
para este dominio para cada valor de la imagen le corresponde un solo valor del dominio
y=5x+2
es una funcion inyectiva, ya que cada valor de y le hace corresponder un solo valor de x,
y=x²
no es una funcion inyectiva, ya que para un determinado valor de y le corresponde 2 valores de x del dominio, por lo tanto podemos hacer una reestriccion del conjunto del dominio de manera que sea inyectiva, haciendo
Domfuncion: x≥0
para este dominio para cada valor de la imagen le corresponde un solo valor del dominio

